题意分析

在浏览网页的时候，缓存技术能够迅速地显示页面。这里我们对浏览器的缓存技术进行简化：我们认为浏览器的缓存大小为M，表示缓存可以存储M个页面。

当用户访问URL时，浏览器会先到缓存中查询是否有该页面的记录，如果有则直接从缓存中提取数据；否则，会发送网络请求，从Internet获取该页面，并将该页面放入缓存中。当缓存中的页面数量超过M时，缓存技术会替换掉缓存中最不频繁访问的网页，即最后访问时间最早的页面。

现在，我们希望对于给定的用户访问历史记录，请判断出每一次访问页面是从缓存中读取的，还是通过网络请求获得的。(缓存最开始数据为空)

算法分析

本题的实质是模拟缓存的工作。

简单的算法

我们直接纯粹的模拟缓存，每当访问一个新的页面时，我们去遍历现在的m条缓存记录。一是确认当前浏览的页面URL是否存在于缓存记录中，二是找出当前缓存记录中最早的一条，并将其替换。

每一次操作的时间复杂度为O(M)，由于一共有N条记录，所以总的时间复杂度为O(NM)。

优化

首先我们可以知道O(NM)中的N是没有办法优化的，所以我们只能从每一次缓存更新入手。

缓存的更新分为两个部分：

• 检查当前是否存在于缓存
• 将缓存记录中最早的一条进行替换

检查当前页面是否存在于缓存

这一个部分我们可以简单的使用map来实现，简单的用Boolean(bool)类型来表示该URL是否在缓存中即可。

将缓存记录中最早的一条进行替换

之前我们采取的方法是通过O(M)的时间进行遍历来查找，如果我们将缓存换用另一种数据结构来进行存储就可以做到O(logN)。

比如二叉树、小根堆等都可以做到。

在这里打算讲的是一种只使用map来完成缓存的更新。

首先我们用a[1..n]来表示浏览网页的记录，用map< url, int > lastVisit的方式来对URL进行记录。

lastVisit[ a[i] ]表示a[i]这条url最后一次访问时对应的时间。

我们知道缓存的大小为M，而且满足了缓存中一定是M个不相同的URL。

假设在我们现在的缓存中最早的一条记录对应的为a[s]，最新的一条记录对应的是a[t]。这样对于第一个问题，检查当前页面是否存在于缓存，我们只需要判定当前i是否在[s,t]这个区间中。

同时可以证明在a[s..t]中至多包含有m条不同的URL。

其证明：

假设a[s..t]中包含有m+1条不同的记录，则我们加入第m+1条记录时，在缓存中是无法找到已经存在的记录。我们一定会抛弃掉缓存中最早的那条记录a[s]，并将其替换为第m+1条记录。所以a[s..t]中一定至多包含m条不同的URL记录。

对于s,t的维护：

t一定总是等于i的，因为a[i]一定是最新的访问记录。

而对于s，我们一定有 lastVisit[ a[s] ] == s。因为若lastVisit[ a[s] ] = k，则一定有k>s，表示该URL在[s+1,t]之中仍存在。若lastVisit[ a[s] ] = s，则表示在[s+1,t]这个区间内都没有a[i]的访问记录了，a[s]则一定是[s,t]这个区间中最早的访问记录。

并且，若此时将a[s]从区间[s,t]中抛弃则表示将这个URL从缓存中抛弃。

所以我们总是要维护lastVisit[ a[s] ] == s。

我们举个例子来说明：

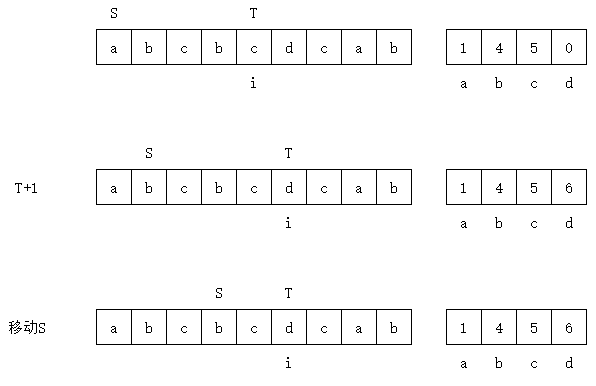
该样例中n=9, m=3。小写的abcd表示4个不同的url。左边表示我们的访问记录，右边表示我们的LastVisit。

当进行到某一步时，S=1,T=5。

此时我们移动T+1，由于第6个网页为d，并不在[s,t]中且m已经到达上限，所以我们需要将a弹出，s+1。同时更新LastVisit[d]，得到中间的一步。

接着我们需要维护s，由于LastVisit[b] = 4, LastVisit[c] = 5，所以2，3位的b和c会被跳过，直到s=4，此时有LastVisit[b] = 4。

这样得到最下面的一幅图，[s,t]完成了更新。

伪代码

s = 1
For i = 1..n
    If (lastVisit[ a[i] ] in [s,i])
        Print "Cache"
    Else
        cacheCnt = cacheCnt + 1;
        If (cacheCnt > m)        // 缓存已满
            s = s + 1            // 将该a[s]从cache中抛弃         
        End If
        Print "Internet"
    End
    lastVisit[ a[i] ] = i    // 更新最后一次访问时间
    While (lastVisit[ a[s] ] != s) 
        s = s + 1
    End While                // 更新s找到新的最早的访问记录  
End For

时间复杂度方面，由于使用了map来维护，所以总的时间复杂度为O(NlogN)

结果分析

该题目的现场通过率为37.5%。200人提交通过了75名选手。

作为该场比赛的第一题，通过率并不是特别高。而本题实际的难度并不大，如果直接从复杂度分析入手应该也能够很容易推到出可行的办法。