题意分析
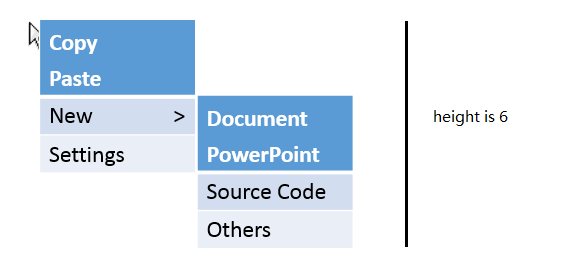
给定一个右键菜单的情况,每一个菜单内选项的数量,以及其子菜单的选项情况。合理的安排整个菜单展开的最大长度最小,输出这个最小值。
算法分析
题目中定义了菜单的元素:
row: 表示一行选项section: 由至少一行row构成,其中row的顺序可以自由排列panel: 由至少一个section构成,其中section的顺序可以自由排列
由于构成panel的元素是固定的,所以一个panel的长度是固定的。所以影响其最大长度因素是该panel内每行row的子菜单长度。
当一行row所展开的子菜单超过该panel的长度时,就会导致整个菜单的总长度被拉长。如何合理的安排row的顺序,使得被拉长的程度最小也就成了解决这道题的关键。
我们从只有从简单的情况开始考虑。
panel只包含有1个section,section包含有 s 行row,记为R1..Rn,但是只有R1有子菜单,且长度为 r。
如果把R1放在第i行,则展开这个子菜单时的长度为 r+i-1 ,所以总的长度为 max( n , r+1-1 )。
因此得到我们的一个结论,有子菜单的row要尽可能往前放置。
panel只包含有1个section,section包含有 s 行row,记为R1..Rn,其中R1有长度为 r1 的子菜单,R2有长度为 r2 的子菜单,且 r1 ≥ r2。
如果把R1放在第i行,R2放在第j行。则展开R1这个子菜单时的长度为 r1+i-1,展开R2这个子菜单时的长度为 r2+j-1。
方案一:i<j,表示R1放在R2前面,此时无法判定 r1+i-1 与 r2+j-1 的大小关系;
方案二:i>j,表示R2放在R1前面,此时一定有 r1+i-1 > r2+j-1。
但是我们有 r1+i-1 ≥ max( r1+i-1 , r2+j-1 ),所以方案一一定不差于方案二。
由此得到我们第二个结论,当有多个包含子菜单的row时,要将子菜单长的尽可能放在前面。
panel只包含有2个section,记为S1,S2。
S1包含有 s1 行row,且展开这些row使得S1最少延伸到 sr1 行(即从S1的第 1 行开始计算,其展开的子菜单最长延伸到第 sr1 行),令 ∆1 = sr1 - s1。举个例子:
+-----------+
| other sec |
+-----------+ - -
| S1 r1 | ^ ^
+-----------+-----------+ | |
| S1 r2 >| | | s1
+-----------+-----------+ | |
| S1 r3 | | sr1 v
+-----------+-----------+ | -
| other sec | | | |
+-----------+-----------+ | ∆1
| | v |
+-----------+ - -
S2包含有 s2 行row,且展开这些row使得S2最少延伸到 sr2 行,令 ∆2 = sr2 - s2。
显然有 sr1 ≥ s1, sr2 ≥ s2。
对于S1和S2来说 s1,_s2_ 是它们的固有长度,它们对总长度的影响,是由 ∆1 和 ∆2 决定的。不妨假设 ∆1 ≥ ∆2。
方案一:S1放在前面,S2放在后面。此时若将S1展开,会使得总长度增加 ∆1-s2;展开S2,会使得总长度增加 ∆2。无法判定 ∆1-s2 与 ∆2 的大小关系。
方案二:S2放在前面,S1放在后面。此时若将S1展开,会使得总长度增加 ∆1;展开S2,会使得总长度增加 ∆2-s1。因为 ∆1 ≥ ∆2 > ∆2-s1 ,所以结果为 ∆1。
可以知道一定有 ∆1 > ∆1-s2, ∆1 ≥ ∆2。因此方案一一定不差于方案二。
由此可以得到我们第三个结论,当有多个section时,我们需要将 ∆ 大的尽可能放在前面。
其中三个结论中,第二个结论实际上包含了第一个结论。而若将row看做只有1行row的section,第二结论其实也和第三个结论等价。所以得到精简的结论:
对于row和section,我们要将子菜单长度与本体长度差值大的靠前放置。
由此我们可以得到对于panel的处理方法:
row:递归处理出每一个row的子菜单长度。section: 将section内的row进行排序,得到section的最优长度方案,记录其本体长度和子菜单长度。panel:将panel内的section进行排序,得到panel的最优长度。
接下来我们来讨论一下具体的实现。
首先可以肯定的是树形结构,下面以C++的代码为例子,我们对三种元素分别建立结构体:
struct row {
int childId; // 子菜单指针
int expandLength; // 子菜单长度
row():childId(-1),expandLength(0) {};
row(int _id):childId(_id),expandLength(0) {};
};
struct section {
vector< row > rows; // 包含的row情况
int selfLength; // 自身的长度 s1
int expandLength; // 展开子菜单之后的长度 sr1
int delta; // 子菜单之后的长度与自身的差值 ∆
section():selfLength(0),expandLength(0),delta(0) {};
};
struct panel {
vector< section > sections; // 包含的section情况
vector< int > rowIds; // 读入时该panel内的rowId
};
读入数据时,我们先将所有row都读入:
panel panels[ MAXN ];
// 读入每一个panel的情况
int n;
cin >> n;
int id, numOfIds;
for (int i = 0; i <= n; ++i) {
cin >> numOfIds;
while (numOfIds--) {
cin >> id;
if (id == 0) ++numOfIds;
panels[i].rowIds.push_back(id);
}
dealPanel( panels[i] ); // 处理panel的情况
}
其中dealPanel函数为:
void dealPanel(panel &p) {
if ( (int) p.rowIds.size() == 0 ) return ;
p.sections.push_back(section());
int sectionId = 0;
// 加入一个末尾0,方便处理最后一个section
p.rowIds.push_back(0);
// 依次出每一个section
for (int i = 0; i != (int) p.rowIds.size(); ++i)
if (p.rowIds[i] != 0) {
p.sections[ sectionId ].rows.push_back( row(p.rowIds[i]) );
} else {
// 新的section
p.sections.push_back(section());
sectionId++;
}
return ;
}
根据我们的上面总结的处理方法,我们可以写出对panel的处理函数:
bool sortByExpandLength(row x, row y) {
return x.expandLength > y.expandLength;
}
bool sortByDelta(section x, section y) {
return x.delta > y.delta;
}
int getExpandLength(panel &p)
{
// ret初始化为0,ret表示该panel的最小展开长度
int ret = 0;
// 枚举每一个section
for (int i = 0; i != (int) p.sections.size(); ++i)
{
// 处理该section内的每一个row的子菜单
for (int j = 0; j != (int) p.sections[i].rows.size(); ++j)
p.sections[i].rows[j].expandLength = getExpandLength( panels[ p.sections[i].rows[j].childId ] );
// 根据row的expandLength对section内的row进行排序
sort(p.sections[i].rows.begin(), p.sections[i].rows.end(), sortByExpandLength);
// 处理得到section的值
p.sections[i].selfLength = (int) p.sections[i].rows.size();
p.sections[i].expandLength = p.sections[i].selfLength; // 展开值至少为selfLength
// 枚举每一个row,找到展开值最大的作为section的展开值
for (int j = 0; j != (int) p.sections[i].rows.size(); ++j)
if (p.sections[i].expandLength < j + p.sections[i].rows[j].expandLength)
p.sections[i].expandLength = j + p.sections[i].rows[j].expandLength;
// 计算section的∆值
p.sections[i].delta = p.sections[i].expandLength - p.sections[i].selfLength;
// 累加panel内所有的row行数作为最小的ret
ret += p.sections[i].selfLength;
}
// 根据section的∆值进行排序
sort(p.sections.begin(), p.sections.end(), sortByDelta);
// now记录当前section的起始行数
int now = 0;
// 枚举每一个section,找到展开值最大的作为panel的展开值
for (int i = 0; i != (int) p.sections.size(); ++i)
{
if (ret < now + p.sections[i].expandLength)
ret = now + p.sections[i].expandLength;
// 累加为下一个section的起始行数
now += p.sections[i].selfLength;
}
return ret;
}
最后我们的答案只需要:
cout << getExpandLength( panels[0] ) << endl;
该段代码还可以以进一步优化,将其中的dealPanel和getExpandLength还可以再合并为一个函数的。
结果分析
本题的通过人数只有3人,提交人数也只有39人。
本题的思维比较巧妙,由于本场比赛总共只有2个小时,大多数选手并没有足够的时间来思考这道题目,可能是导致该题通过率较低的主要原因。

根据题解来看,如果一个panel中有多个row有子菜单,那么其“长度”应该是由那些使得展开row最长的情况来记录,题目要求的是重新安排row和section,使得这些最长的情况最短。不知我理解的是否确切?