题意分析

小Hi和小Ho正在玩这样一个游戏，在每局游戏的开始，小Hi手持一瓶可以认为是无穷无尽的饮料，而小Ho手中有一个空杯子。

一局游戏分为N轮，在每轮行动中，小Hi先向小Ho手中的杯子倒入T个单位的饮料（倒入的数量在一局游戏开始之前约定好且在整局游戏中固定），然后小Ho掷出一个均匀的K面骰子得到一个1..K之间的数d，如果杯中饮料的单位数小于等于d，则小Hi记一分，且小Ho将杯中剩余饮料一饮而尽，否则小Ho记一分，小Ho喝掉杯中d个单位的饮料。在N轮结束后，分高者获胜。

那么问题来了，如果小Ho能够预测这局中每轮自己所掷出的点数，那么最小的能使得小Ho获胜的T（每轮小Hi倒入小Ho杯子的饮料的单位数）是多少？

算法分析

本题需要我们求的是最小满足要求的 T 值，使得在该 T 值下，小Ho获得的分数高于小Hi。

因为小Hi和小Ho分数之和一定为 n，所以小Ho获胜的条件可以改为小Ho的分数score大于n/2。

通过分析题意，我们可以知道score和 T 之间满足一定的关系，score会随着 T 值的变化而变化，则可以假设有：

score = f(T)

我们根据题目描述的游戏规则构造出f(T)函数：

f(T):
    rest = 0;     // 当前杯中剩余的饮料体积
    score = 0;    // 小Ho的得分
    for i = 1 .. n
        rest = rest + T;    // 小Hi向杯子中倒入T单位饮料
        if (rest > d[i])    // 若杯子中饮料大于第i轮的d
            score = score + 1;     // 小Ho获得一分
            rest = rest - d[i];    // 小Ho喝掉d个单位饮料
        else
            rest = 0;       // 小Ho喝掉全部的饮料
        end if
    end for
    return score;

每次执行f(T)函数花费的时间代价为 O(n)。

对f(T)进一步研究，我们可以发现：

• 当 T = 0 时，score = f(0) = 0
• 当 T = K+1 时，score = f(K+1) = n

我们可以猜想在 T 从 0 到 K 的过程中，小Ho获得的分数score是单调递增的。

而要证明f(T)函数确实满足递增的性质，只需证明对于 T 和 T' (T < T')，每一轮开始时小Ho的得分和剩余的饮料体积，T 对应的数值都不超过 T' 对应的数值。

我们设s[i]，r[i]表示第i轮开始，还没有添加 T 单位饮料时，小Ho的得分和剩余饮料的体积；s'[i]，r'[i]表示第i轮开始，还没有添加 T' 单位饮料时，小Ho的得分和剩余饮料的体积。

我们要证明：对于i = 1..N+1，都有s[i] ≤ s'[i]且r[i] ≤ r'[i]。

利用数学归纳法，i = 1 时，s[i] = s'[i] = 0，r[i] = r'[i] = 0，结论成立。

假设i = n 时结论成立，那么当i = n+1 时：r[n+1] = max(r[n]+T-d, 0), r'[n+1] = max(r'[n]+T'-d, 0)。

由于r[n] ≤ r'[n]，T < T'，所以r[n]+T < r'[n]+T'

• 当d < r[n]+T < r'[n]+T时，r[n+1] = r[n]+T-d, r'[n+1] = r'[n]+T'-d, s[n+1] = s[n]+1, s'[n+1] = s'[n]+1，易知结论成立；
• 当r[n]+T ≤ d < r'[n]+T时，r[n+1] = 0, r'[n+1] = r'[n]+T'-d > 0, s[n+1] = s[n], s'[n+1] = s'[n]+1，易知结论成立；
• 当r[n]+T < r'[n]+T ≤ d时，r[n+1] = r'[n] = 0, s[n+1] = s[n], s'[n+1] = s'[n]，易知结论成立。

综上所述，对于i = 1..N+1，都有s[i] ≤ s'[i]且r[i] ≤ r'[i]。而f(T) = s[N+1] ≤ s'[N+1] = f(T')，所以函数f(T)是单调递增的。

当score首次超过n/2时的 T 值，也就是我们要求的最小值，不妨记为 M。

那么接下来要考虑的就是如何快速的求得 M 值。

一个简单的想法是从 0 开始依次枚举，直到score大于n/2，这样可以保证在第一时间计算出 M 值。一共需要执行 M 次f(T)函数，所以其时间复杂度为 O(nM)。对于足够强的数据这显然是会超时的，必须降低执行f(T)函数的次数。

我们再一次观察f(T)函数：

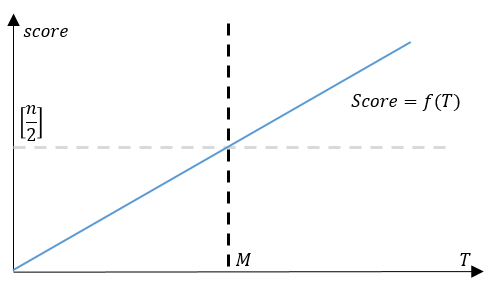
我们随机找一个 T 值，并计算出其f(T)。根据f(T)与n/2的大小关系，我们可以判断出当前计算出的 T 值是小于 M，亦或是大于 M。

由这个性质，我们可以得到一个区间逼近的算法：

1. 初始化 T 可能的取值区间[left, right]，保证f(left) < n/2, f(right) ≥ n/2。这里我们取[0,M]。
2. 若left + 1 == right，跳转第四步。否则继续第三步。

3. 取 mid = (left + right) / 2，并计算出f(mid)。

   假设f(mid) < n/2，由f(T)为单调递增函数，则对于任意一个 T 属于[left, mid]，f(T) < n/2。

   因此 M 一定不在[left, mid]内，M 一定在[mid, right]的区间内。因此我们令left = mid，并回到第二步。

   同理，若f(mid) ≥ n/2，则 M 一定在[left, mid]。此时我们令right = mid，并回到第二步。

4. 由于left + 1 == right，且f(left) < n/2, f(right) ≥ n/2。因此right即为所求的 M 值。

这个算法满足每一次将区间缩小一半，因此总的时间复杂度为 O(nlogK)。其伪代码：

left = 0;
right = K;
while (left + 1 < right)
    mid = (left + right) / 2;
    if (f(mid) < n/2) left = mid;
    else right = mid;
end while

至此我们得到了该题的解决办法：利用二分缩小答案的区间，并利用答案本身去判定最优解的范围。

这样的算法我们一般称之为"二分答案"，其明显的标志有两个：

• 求可行解中的最优解
• 能够构造出关于解的f(T)函数，并且f(T)函数满足单调性

只要能够熟练的发现这两个标志，对于同类的问题也就能够迎刃而解了。