hiho一下第78周《Shortest Proper Prefix》题目分析

0
0

题目大意

给定N个单词，求满足下列条件的前缀集合S：

  • 集合中任意前缀对应的单词数量小于等于5
  • 对于集合中任意前缀p，p的扩展前缀不属于该集合

对于第二个条件，举个例子来说：

假设ab对应了5个单词，abc对应了3个单词，abd对应了2个单词。

因为ab对应的单词数量少于等于5，所以ab属于集合S。虽然abc和abd对应的单词数量均小于等于5，但由于其为ab的扩展，所以不属于S。

解题思路

由于本题需要询问多个单词的公共前缀，很显然的是一道Trie树的题目，关于Trie树的讲解，可以点击这里学习。

首先我们将所有的单词建立成一颗Trie树，举个例子：

pic1

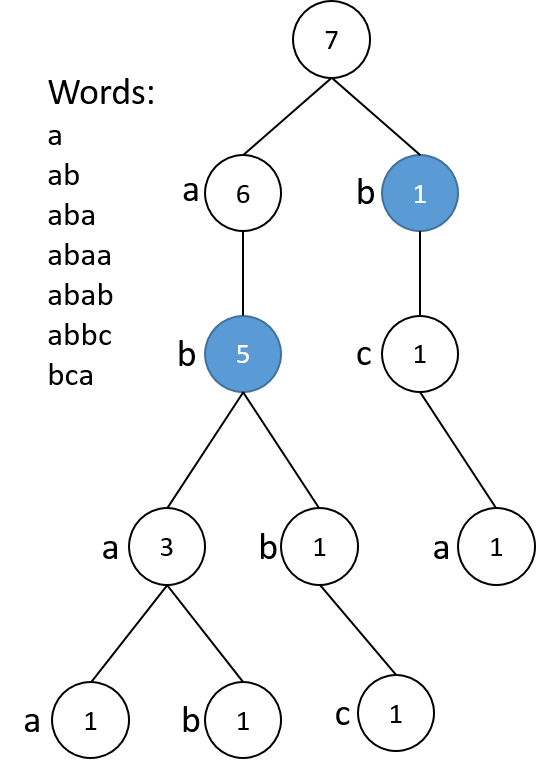
对于树上任意一个节点，表示从根到节点路径构成的前缀，其数字表示该前缀对应的单词数量。

题目中描述的两个条件很容易在该Trie树中判定：

  • 当节点数字小于等于5时，则表示该前缀是一个合法解
  • 当节点为合法解时，以它为根的子树上其他节点都不再计入合法解

在上图中，蓝色节点表示最后属于集合S的前缀。

由此我们可以得到一个简单的算法：

  1. 对构建好的Trie树进行遍历
  2. 若当前节点计数小于等于5，返回1
  3. 若当前结点计数大于5，递归对所有子树进行遍历，并返回统计和

写成伪代码为：

Traversal(root)
    If (root.cnt <= 5)
        Return 1
    End If
    total = 0
    For i = 'a' .. 'z'
        If root.chd[i] is not empty
            total = total + Traversal(root.chd[i])
        ENd If
    End For
    Return total

到此，本题也就顺利的解决了。

  • 如果a的子树有ca前缀，b的也有，是不是应该存在ca前缀，但是这个树却得不到

  • 添加评论
  • ✖reply

5 answer(s)

0 
private static final int COUNT_LIMIT = 5;

public static void main(String[] args) {
    String[] str = { "a", "ab", "aba", "abaa", "abab", "abbc", "bca" };
    ShortestProperPrefix spp = new ShortestProperPrefix();
    List<String> res = spp.shortestPrefix(Arrays.asList(str));
    System.out.println(res);
}

// "" is a prefix; consider duplicated words not.
public List<String> shortestPrefix(List<String> words) {
    List<String> res = new ArrayList<>();
    TrieNode root = buildTrie(words);
    preorderTraverse(res, "", root);
    return res;
}

private void preorderTraverse(List<String> res, String string, TrieNode root) {
    if (root == null) {
    } else if (root.count <= COUNT_LIMIT) {
        res.add(string);
    } else {
        for (Map.Entry<Character, TrieNode> e : root.child.entrySet()) {
            preorderTraverse(res, string + e.getKey(), e.getValue());
        }
    }
}

private TrieNode buildTrie(List<String> words) {
    TrieNode root = new TrieNode();
    root.add(words);
    return root;
}

private class TrieNode {
    private int count;
    private Map<Character, TrieNode> child;

    TrieNode() {
        this.count = 0;
        this.child = new HashMap<>();
    }

    public void add(List<String> s) {
        for (String e : s) {
            add(e);
        }
    }

    public void add(String s) {
        add(s, 0);
    }

    private void add(String s, int i) {
        count++;
        if (i < s.length()) {
            Character c = Character.valueOf(s.charAt(i));
            if (child.get(c) == null) {
                child.put(c, new TrieNode());
            }
            child.get(c).add(s, i + 1);
        }
    }
}
0

12 a ab abc abcde abcde abcba bcd bcde bcbbd bcac bee bbb

最后公共前缀 ab 5 cd 3 de 3 bb 2 ca 1 ac 1 不对吗

0 
#include <iostream>
#include <string.h>
#include <string>

using namespace std;
typedef struct node trie;

typedef struct edge{
    char ch;    //该边表示的字母
    trie *child;   //指向的节点的指针
    edge *next; //下一条边

}edgelist;
struct node{
    int n;      //以该节点为根节点的树包括的单词数量
    int sn;     //表示该节点是否是一个词尾
    edgelist edges; //边的列表头结点
};

trie root;
trie * add_ch(char x, trie *rt)
{
    edge * p = &(rt->edges);
    while(p)
    {
        if(p->ch == x)
            return p->child;
        p = p->next;
    }
    p = &(rt->edges);
    while(p->next) p = p->next;
    p->next = new edge;
    memset(p->next, 0, sizeof(edge));
    p->next->ch = x;
    p->next->child = new node;
    memset(p->next->child, 0, sizeof(node));
    return p->next->child;
}
void add_word(const string &word)
{
    trie *proot = &root;
    for(int i=0; i<word.length(); ++i)
    {
        proot = add_ch(word[i], proot);
        proot->n += 1;
    }

    proot->sn = 1;

}
int query2(trie * rt)
{
    if(rt->n <=5)
        return 1;
    int sum = 0;
    edge *p = rt->edges.next;
    while(p)
    {
        sum += query2(p->child);
        p = p->next;
    }
    return sum;
}
int main()
{
    int n;
    cin >>n;
    root.n = n;
    while(n--)
    {
        string word;
        cin >> word;
        add_word(word);
    }
    int sum = 0;
    edge *p = root.edges.next;
    while(p)
    {
        sum += query2(p->child);
        p = p->next;
    }
    cout << sum;
    return 0;
}
1

楼主你好，我想了解下我的这段代码为什么是RE，在本地测试没有问题呢。

#include<string>
#include <iomanip>
#include<fstream>
#include<set>
#include<queue>
#include<map>
//#include<unordered_set>
//#include<unordered_map>
//#include <sstream>
//#include "func.h"
//#include <list>
#include<stdio.h>
#include<iostream>
#include<string>
#include<memory.h>
#include<limits.h>
//#include<stack>
#include<vector>
#include <algorithm>
using namespace std;

struct TrieNode{
    int count;
    vector<TrieNode*> child;
    TrieNode() :count(0), child(26,NULL){};
    TrieNode(int x) :count(x), child(26,NULL){};
};
//插入单词
void InsertWord(char *a, int pos, TrieNode*p)
{
    if (a[pos] == 0) return;//已经遍历完毕
    else
    {
        //如果不存在，则新建儿子节点
        if (p->child[a[pos] - 'a'] == NULL)
            p->child[a[pos] - 'a'] = new TrieNode();
        p->child[a[pos] - 'a']->count++;
        InsertWord(a, pos + 1, p->child[a[pos] - 'a']);
    }
}

//深度搜索
void dfs(int &ans, TrieNode*root)
{
    //如果计数小于5，则不再遍历其儿子节点
    if (root->count <= 5)
        ans++;
    else
    {
        //循环遍历儿子节点
        for (int i = 0; i < 26; i++)
        {
            if (root->child[i])
            {
                dfs(ans, root->child[i]);
            }
        }
    }
}
/*
函数名  ：main
函数功能：主函数
*/
int main(void)
{
    int n;
    TrieNode *root = new TrieNode;
    root->count = INT_MAX;
    char *word = new char[10000];
    memset(word, 0, 10000);
    cin >> n;

    //输入单词
    for (int i = 0; i < n; i++)
    {
        memset(word, 0, 10000);
        scanf("%s", word);
        InsertWord(word, 0, root);
    }

    //进行深度搜索
    int ans = 0;
    dfs(ans, root);
    cout << ans << endl;

    return  0;
}

  • 找到原因了，word分配的数组不够大，改为 char *word = new char[1000000];就可以了

  • 添加评论
  • ✖reply
0
  • List itemvfsad vfsfv

write answer 切换为英文 切换为中文

转发分享

▲