题目大意

小hi超级电脑的电源出问题了。因为是超级电脑，所以电源组件很多了，一共有N个（编号1~N）。但是当某些电源组件同时开启或同时关闭时，电路就出错了！由于是超级电脑，所以只要有至少一个电源组件开启也是能启动的。小hi只好决定关掉其中一部分电源组件，让电脑先启动起来。

解题思路

该题的本质为2-SAT问题。

2-SAT通常被描述为这样：给定N对物品，每对物品中必须选择且只能选择一个。物品之间有一些限制关系，询问是否选出N个物品满足所有的限制关系。

对应到本题，即是每一个电源有两种可选状态，关闭(1状态)和打开(0状态)。限制状态被描述为当两个电源不能同时打开或关闭。选出物品即对应找到一个合法的状态。

对于该题，解决方案为：

根据N的值建立一个包含2N个点图，分别表示N个点的0状态和1状态。若存在(i,j)之间的限制关系：

• i与j不能同时为0。存在2种限制关系：
  • 若选择i1，则一定要选择j0；
  • 若选择j1，则一定要选择i0； 因此连接有向边<i1,j0>,<j1,i0>。
• i与j不能同时为1。存在2种限制关系：
  • 若选择i0，则一定要选择j1；
  • 若选择j0，则一定要选择i1； 因此连接有向边<i0,j1>,<j0,i1>。

举个例子：

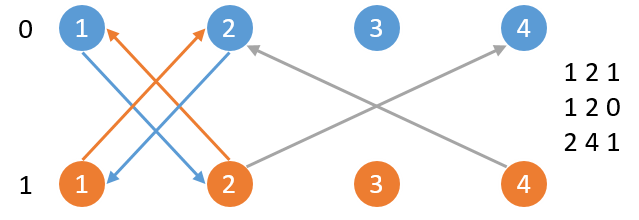
每一个颜色的边，对应原数据中一个限制关系。

根据上面规则我们得到了一个包含有限制关系的有向图。我们考察这个有向图的强连通分量，如果存在一对点i0和i1在一个强连通分量里，那么意味着选i0必选i1，选i1必选i0，无解。否则如果每对点都在不同的强连通分量，那么一定有解。

该算法的正确性证明可以参考2-SAT问题解析或者Aspvall, Plass & Tarjan (1979)

寻找有向图的强连通分量，你可以在Hiho一下第54期找到强连通分量的讲解。

那么来总结一下本题的解法： 1. 根据读入的信息，建立有向图以及各条限制关系对应的有向边 2. 进行强连通分量的求解 3. 判断是否有同一个点i的两个状态,i0和i1属于同一个强连通分量

由于本题输入数据有多组，所以一定要记得初始化。