hiho一下第81周《Professor Q's Software》题目分析

2
1

题目大意

Q老师编写的软件中存在着N个模块，依次编号为1..N，其中编号为i的模块会在接收到一个名称为Signal[i]的信号时启动，对于不同的模块，他们启动需要的信号可能是相同的。 在这N个模块里，代码的执行也会触发若干(K<=5)信号，这些信号又可能会导致其他模块的启动，从而使得整个软件运转起来，但值得庆幸的是，模块间的互相启动是不存在循环的，也就是无论收到什么样的信号，这个软件最终都会停止运行。 现在Q老师为了测试整个软件，使用特定的工具发出了M个信号，而他希望能够知道，每个模块应该被运行的次数。

解题思路

通过题意，我们首先可以确定，不同模块之间可以按照以下原则构成一个有向无环图：

  • 初始信号流，即 M 个初始信号，我们将其设定为模块0发出的信号
  • 若模块i发出的信号能够使得模块j被激活，我们连接一条从i到j的有向边(i,j)

比如数据：

3 2
123 256
123 2 456 256
456 3 666 111 256
256 1 90

对应的图为：

pic1

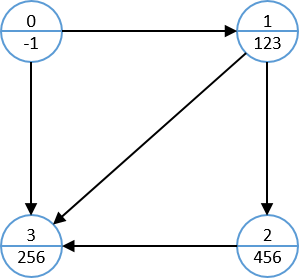
由于原题中给出的信号在0~10^5之间，因此我们可以用一个大小为10^5的数组signList来记录信号可以激活的模块，辅助我们构造整个图：

Input n
Input m
// 将初始数据流做为 module 0
For i = 1 .. m
    Input sign
    module[0].sendSign.push(sign)
End For
// 读取其他module的信息
For i = 1 .. n
    Input sign
    module[i].activeSign = sign
    signList[ sign ].canActiveModule.push(i)
    Input num
    For j = 1 .. num
        Input sign
        module[i]sendSign.push(sign)
    End For
End For
// 构造有向无环图
For i = 0 .. n
    For sign in module[i].sendSign
        For j in signList[ sign ].canActiveModule
            addEdge(i, j)
        End For
    End For
End For

在得到有向无环图之后，一个简单的做法是直接在上面做一次DFS，去统计每个点被访问到的次数：

DFS(nowModule):
    If (nowModule not 0) Then
        activeCount[ nowModule ] = activeCount[ nowModule ] + 1
    End If
    For each j in (nowModule, j)
        DFS(j)
    End For

该算法的时间复杂度非常高，但由于本题没有设计专门针对的数据，所以在测试时也能通过所有的测试点。

但是显然这不是我们要的最优算法，本题实际考察的算法为拓扑排序(toposort)。

利用拓扑排序，在O(n + m)的时间内计算出所有点被访问的次数，具体的算法讲解可以参见hiho一下第48期

在本题中，访问次数对应的为第48期题目中的病毒数量。因此我们在构造完图之后，可以使用同样的算法来解决：

// 在构造图时同时统计入度
For i = 0 .. n
    For sign in module[i].sendSign
        For j in signList[ sign ].canActiveModule
            addEdge(i, j)
            inDegree[j] = inDegree[j] + 1
        End For
    End For
End For

// 进行拓扑排序
tail = 0;
For i = 0 .. n  // 这里一定要从0开始，因为Module 0也是图中的点
    If (inDegree[i] == 0) Then  // 入度为0的点
        sequence[tail] = i
        tail = tail + 1
    End If
End For

activeCount[0] = 1  // 设定初始信号流的访问次数为1
activeCount[1 .. n] = 0
i = 0
While (i < tail) Then
    nowModule = sequence[i]
    For each j in (nowModule, j)
        activeCount[j] = activeCount[j] + activeCount[ nowModule ]
        inDegree[j] = inDegree[j] - 1
        If (inDegree[j] == 0) Then
            sequence[tail] = j
            tail = tail + 1
        End If
    End For
    i = i + 1
End While

最后再将activeCount数组依次输出即可。由于本题有多组数据，在实现时一定要注意初始化。

4 answer(s)

1

有没有考虑到一个模块可能会发出去几个相同的信号

0

我觉得有一点需要注意，在开始拓扑排序时可能存在多个入度为0的点，如下图： enter image description here

照道理应该只从节点0开始发送信号，即加入拓扑排序的队列。但节点3没有输入信号，所以节点3不会被遍历到，从而节点2的入度不会减至0，若节点2还有后继节点，那么将不会被遍历到，答案会出现错误。所以在开始拓扑排序前需要将所有入度为0的节点都加入队列。

0

@lucienwang 我还是贴代码吧，帮忙找找问题出在哪。。。多谢！

#include<stdio.h>
#include<stdlib.h>

/*
 * Record signal message in linktable. This is the defination 
 * of linktable node. The input signal is the index of array: signals.
 * Parameters:
 *      @input: The number of signals that can call this singal.
 *      @value: The value of this signal.
 *      @next: The pointer of the output of this signal.
 *      @count: The number of calling of this signal.
 */
typedef struct node1 {
    int input;
    int value;
    struct node1* next;
    int count;
} signal;

// The signals list. 
signal signals[100005];

// The module list, the element is the input signal of each module.
int modules[100005];

// The number of modules. 
int N;

/* 
 * This fuction deals with one test case.
 * Parameters:
 *      None.
 * Return:
 *      None.
 */ 
void function(void);

/*
 * This function initial the situation for one test case.
 * Parameters:
 *      None.
 * Return:
 *      None.
 */
void init(void);

/*
 * This function adds one output signal of a signal.
 * Parameters:
 *      @input: The input signal.
 *      @output: The output signal number to add.
 */
void add_output_signal(int input, int output);

/*
 * This function calculates the number of each module calling.
 * Parameters:
 *      @input: The input signal.
 * Return:
 *      None.
 */
void calculate(int input);

/*
 * This function print the result of one test case.
 * Parameters:
 *      None.
 * Return:
 *      None.
 */
void print_result(void);

/*
 * The main program.
 */
int main(void) {
    int T;
    scanf("%d", &T);

    for(int i = 0; i < T; i++) {
        function(); 
    }

    return 0;
}

/* 
 * This fuction deals with one test case.
 * Parameters:
 *      None.
 * Return:
 *      None.
 */ 
void function(void) {
    init();
    int M;
    scanf("%d %d", &N, &M);

    signals[100001].input = 0;
    signals[100001].count = 1;
    int s;
    for(int i = 0; i < M; i++) {
        scanf("%d", &s);
        add_output_signal(100001, s); 
    }

    int S, K, E;
    for(int i = 0; i < N; i++) {
        scanf("%d %d", &S, &K);
        modules[i] = S; 
        for(int j = 0; j < K; j++) {
            scanf("%d", &E);
            add_output_signal(S, E);    
        }
    }

    int tag = 1;
    while(tag == 1) {
        tag = 0;
        for(int i = 0; i < 100005; i++) {
            if(signals[i].input == 0) {
                tag = 1;
                calculate(i);
            }
        }
    }
    print_result();
}

/*
 * This function initial the situation for one test case.
 * Parameters:
 *      None.
 * Return:
 *      None.
 */
void init(void) {
    for(int i = 0; i < 100005; i++) {
        signals[i].input = -1;
        signals[i].value = i;
        signals[i].count = 0;
        signals[i].next = NULL;
        modules[i] = 0;
    }
    N = 0;
}

/*
 * This function adds one output signal of a signal.
 * Parameters:
 *      @input: The input signal.
 *      @output: The output signal number to add.
 */
void add_output_signal(int input, int output) {
    signal* s = (signal*) malloc(sizeof(signal));
    s->value = output;

    s->next = signals[input].next;
    signals[input].next = s;

    signals[output].input++;
    if(signals[output].input == 0) {
        signals[output].input++;
    }
}

/*
 * This function calculates the number of each module calling.
 * Parameters:
 *      @input: The input signal.
 * Return:
 *      None.
 */
void calculate(int input) {
    signal* p = signals[input].next;
    while(p != NULL) {
        signals[p->value].input--;  
        signals[p->value].count += signals[input].count;
        if(signals[p->value].count >= 142857) {
            signals[p->value].count %= 142857;
        }
        p = p->next;
    }
    signals[input].input = -1;
}

/*
 * This function print the result of one test case.
 * Parameters:
 *      None.
 * Return:
 *      None.
 */
void print_result(void) {
    for(int i = 0; i < N; i++) {
        printf("%d ", signals[modules[i]].count);
    }
    printf("\n");
}
2

有谁能給组测试数据? 已经WA了很多次了T-T

write answer 切换为英文 切换为中文

转发分享

▲