题目大意
给定N个点,编号为1..n,坐标分别为(x[i], y[i])。两个点的距离为:
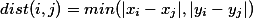
求一条路径从点1到点n,使得路径总距离最短。
解题思路
本题求解从点1到到点n的最近距离,很显然是一个单源点最短路径问题,因此我们考虑使用Dijstra或是SPFA来进行求解。
但由于题目中 N 的最大范围为 100,000,因此边的最大可能数量为 4,999,950,000。显然直接使用最短路径算法进行计算会超时,我们需要对图进行优化。
缩点
任意两个点距离为:
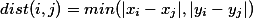
因此存在两个点i,j,x[i]==x[j]或y[i]==y[j],则dist(i,j) = 0。
我们将所有互相之间距离为0的点构成一个集合,称为团。
对于团内任意两个点,其距离均为0。
那么如何来构造出团呢?
- 首先对所有点的x的坐标进行排序
- 遍历排序后的x点坐标,若有连续一段的x值都相等,则我们将这一段中所有点都与第一个点(将这个点称为代表点)连边,距离为0
伪代码为:
sort(x)
i = 1
While (i ≤ n) Then
j = i + 1
While (j ≤ n and x[i].val == x[j].val) Then
连接边(x[i].id, x[j].id, 0) // 因为无向图,所以需要连接两条边
j = j + 1
End If
i = j
End While
同理我们处理完x坐标后,再对y坐标进行同样的处理。
在处理后,我们可以保证:对于团内任意两点,其最短路径距离为0。
并且除代表点外每个点至多连接有2条边,总边数不超过O(N)。
最近距离
在本题中,最近距离的处理上,还有另一个很重要的性质:
对于任意一个点i,在x坐标和y坐标排序后,坐标值不等于点i,且最靠近点i的点。我们称为点i的邻居。如下图中所示的绿色点:
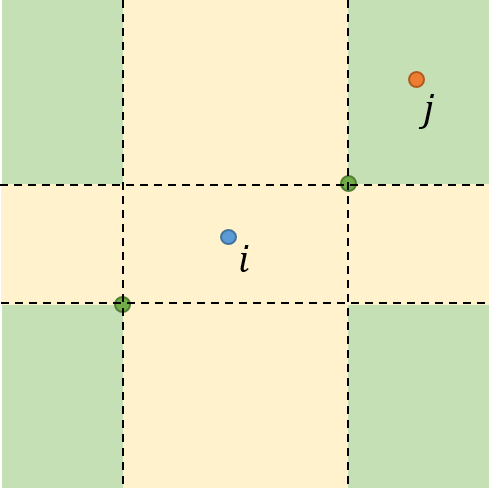
通过该图可以知道,邻居节点一定是在虚线的交点处,因此对于点i,邻居节点至多有4个。并且在图中黄色的区域,也就是点i的上下左右4个区域内是不存在其他点的。其他点只能存在于绿色的区域内。
假设有一个点j,存在于绿色区域内,可以证明从点j直接到点i的距离一定不会优于点j先到邻居节点再到点i。
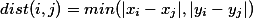
通过邻居节点则:
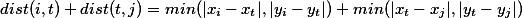
由于:
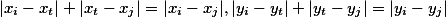
因此有:
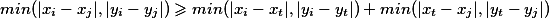
所以我们并不需要将点i和点j的边进行连接,只需要连接点i和邻居节点的边即可。
伪代码:
sort(x)
i = 1
While (i ≤ n) Then
j = i + 1
While (j ≤ n and x[i].val == x[j].val) Then
j = j + 1
End If
If (j ≤ n) Then
连接边(x[i].id, x[j].id, x[j].val - x[i].val)
End
End While
同时再处理y坐标。
对于每一个点,连接了2个x值最靠近的点,2个y值最靠近的点。在这次处理后新增加的边数不超过O(N)。
通过上面这两条处理,我们构造了图,并且图中边的数量为O(N)级别,此时再使用Dijstra或者SPFA这一类的单源点最短路径,即可在限定时间内求解。

邻居节点不是很理解;如果它前提是x,y值都不相等的话,那黄色区域中可以有其它点,比如某点和i是同x轴的;而如果它前提是x,y值有一个不同就可以,那某点和i是x相等的就是邻居节点,这时候它可以大于4。所以三角定理是不成立的