题目大意

小Hi在时刻T到达了室内游泳池。 游泳池一共有N条泳道，游泳池两侧分别标记为0和1。 已知除了小Hi，一共有Q个其他游泳者。每个游泳者有自己的游泳计划(t,l,n,d)，表示他会在t时刻从游泳池d侧进入泳道n，花费l个单位时间到达对面。 小Hi从一侧到达另一侧的时间为L，一开始小Hi在0侧。 现在小Hi想要从两侧来回游泳，一共游R趟。 根据其他人的计划，求问小Hi在保证不和其他人相撞的情况下，最早何时能够游完这R趟。

解题思路

本题是一道模拟类的题目，需要枚举时间点，然后判定是否存在一条泳道能够允许小Hi完成游泳。

一个简单的算法是直接枚举每一个时间点，依次检查是否存在一条可以使用的泳道：

time = T        // 时间点
direction = 0   // 游泳的方向
while (R > 0)
    found = false
    For lane = 0 .. N-1  // 枚举泳道
        If canSwim(time, lane, direction) Then
            found = true
            break
        End If
    End For
    If (found) Then
        direction = 1 - direction
        // 游到了对岸，所以方向需要改变
        time = time + L
        R = R - 1
    Else
        time = time + 1
    End If
End While

考虑到canSwim函数的时间复杂度在O(Q)级别，仅仅在现有的数据范围下，可以发现time可能达到 10^4 数量级，而N可能达到10^3 数量级，整个算法的复杂度在10^7*O(Q)。

此外还需要考虑到多组数据的情况，上面的算法几乎可以肯定会超过时间限制。

通过观察，我们可以发现上面算法很多冗余的计算是浪费在time = time + 1这一步，为了减少时间累积的次数，我们要做的是找出一系列时间点，而不是依次去枚举。

那么，我们需要找的是什么样的时间点呢？

假设，现在只有1条泳道，只有1个人要游泳，他的计划是时间t下水，经过l个单位时间到达。

我们用一个图来表示这个人的游泳时间：

其中上下两侧各为一根黑色时间轴，从左到右对应了时间0..infinite。同时上下也表示游泳池的两侧。

时间轴之间的蓝色向量表示这个人游泳的时间和位置的对应关系，箭头的方向表示他游泳的方向。我们把这个向量不妨称为事件向量(event)

接下来我们需要在这个图上标记出小Hi的事件向量。很显然，该图中可以标记处无数个小Hi的事件向量，但我们最关注的只有2个：

• 若在这个人之前下水，小Hi最晚可以出发的时间所对应的事件向量，称为最晚事件向量
• 若在这个人之后下水，小Hi最早可以出发的时间所对应的事件向量，称为最早事件向量

同时我们还需要考虑另外两个因素：

• 小Hi和这个人速度的区别，即L和l的大小关系
• 小Hi和这个人方向的区别，即同向还是异向

由此可以得到以下6个图，其中橙色表示小Hi的事件向量：

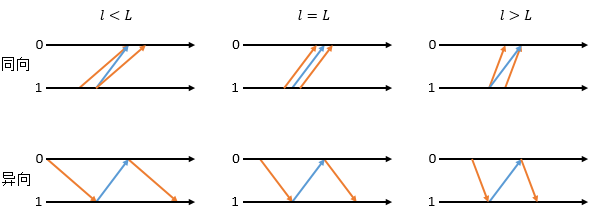
那么我们找这个最早和最晚事件向量有什么意义呢？

我们不妨假设最晚事件向量起始的时间为t1，最早事件向量起始的时间为t2。则对于小Hi而言除了t1~t2这个时间段以外，其他任意时间段都是可以使用的。

若我们设定一个值x，初始为x=0。当我们枚举时间t时，若经过了t1，则将x+1，经过t2，则将x-1。这样我们就可以直接通过x的值来判断，当前泳道是否可以使用。若x=0则当前泳道可以使用，否则不可以。

所以在判定泳道是否可以使用时，只需要关注这两个事件向量。

又由于速度是可以确定的，而方向是不确定的(因为并不知道这个人游泳的时候，小Hi在游泳池0这一侧还是1这一侧)。因此对于这个人来说，我们需要记录的是同向的两个事件向量(最早和最晚)和异向的两个事件向量。共记4个事件向量。

我们建立数组eventSequence[2]来记录我们关注的事件向量，eventSequence[0]表示小Hi在游泳池0侧时，所产生的事件向量；eventSequence[1]表示小Hi在游泳池1侧时，所产生的事件向量。

由于每一个游泳者会使得小Hi产生2个事件向量，因此eventSequence[0]和eventSequence[1]各会记录2N个事件向量。

eventSequence中的每个元素event包含3个属性：

• t: 出发时间
• n: 使用的泳道
• x: 该事件向量的类型，1表示该事件向量为最晚事件向量，-1表示该时间为最早事件向量。

其处理的伪代码为：

addEvent(t,l,d,n)
    // t表示游泳者的出发时间
    // l表示游泳者游泳的持续时间
    // d表示游泳者的方向，只能为0或1
    // n表示游泳者所选取的泳道

    // 首先考虑同向时，根据速度不同进行分类

    If (l < L) Then
        eventSequence[d].add({  // 最晚事件向量
            t: t + l - L, // 同时到达对岸
            n: n, x: 1
        })
        eventSequence[d].add({  // 最早事件向量
            t: t, // 同时出发，因为小Hi速度慢，追不上游泳者
            n: n, x: -1
        })
    Elseif (l == L) Then
        eventSequence[d].add({  // 最晚事件向量
            t: t + 1, // 晚1个单位时间出发
            n: n, x: 1
        })
        eventSequence[d].add({  // 最早事件向量
            t: t - 1, // 早1个单位时间出发
            n: n, x: -1
        })
    Elseif (l > L) Then
        eventSequence[d].add({  // 最晚事件向量
            t: t, // 同时出发，因为小Hi速度快，游泳者追不上
            n: n, x: 1
        })
        eventSequence[d].add({  // 最早事件向量
            t: t - 1 - L, // 同时到达对岸
            n: n, x: -1
        })
    End If

    // 异向时，无论如何也得等对面游完
    eventSequence[1 - d].add({  // 最晚事件向量
        t: t - L, // 小Hi到达对岸时，游泳者出发
        n: n, x: 1
    })
    eventSequence[1 - d].add({  // 最早事件向量
        t: t + l, // 游泳者到达后，小Hi出发
        n: n, x: -1
    })

由于我们仍然需要按时间来进行枚举，因此需要对eventSequence进行排序，时间小的考前，当时间相同时，考虑将最早事件向量往前放置。

即排序条件为 event1.t < event2.t 或者 event1.t == event2.t and event1.x < event2.x，event1在event2之前。

又因为在实际中泳道不止一条，所以我们不能用一个单纯的x来表示，因此我们设立一个数组lane[2][N]，lane[0][i]表示当前时刻对于泳道i，从游泳池0侧出发，会影响到小Hi游泳的人数。同理lane[1][i]表示从游泳池1侧出发。

加入eventSequence和lane之后，我们的主函数变为：

time = T        // 时间点
direction = 0   // 游泳的方向
point[2] = {0, 0} // 两个方向已经处理过的事件数量
while (R > 0)
    found = false
    // 循环处理的事件向量
    While (point[ direction ] < 2*N) Then
        // 获取这个事件向量event
        event = eventSequence[ direction ][ point[ direction ] ];
        If (event.t < time) Then
            // 当前时间已经经过了这个事件向量的时间
            // 因此修改对应'x'的值
            lane[ direction ][ event.n ] = lane[ direction ][ event.n ] + event.x
            // 指针后移
            point[ direction ] = point[ direction ] + 1
        Else
            // 当前时间未超过这时间向量
            // 首先查看在T~event.t这段期间内能不能找到可以使用的泳道
            // 直接检查lane
            For i = 0 .. N-1
                If (lane[ direction ][i] == 0) Then
                    // 有可以使用的泳道
                    found = true
                    // 使用该泳道并增加时间
                    time = time + L
                    Break
                End If
            End For
            If (found) Then
                // 若找到泳道，则可以跳出当次循环，保留当前event
                Break
            End If
            // 此时表示在T~event.t这段时间内均没有可以使用的泳道
            // 则我们直接将时间T推移至event.t，并执行这个事件向量
            time = event.t
            lane[ direction ][ event.n ] = lane[ direction ][ event.n ] + event.x
            // 指针后移
            point[ direction ] = point[ direction ] + 1
        End If
    End While
    If (!found) Then
        // 会出现found为false的情况，则表明该方向所有的event都已经结束
        // 此时只有小Hi一个人还在游泳
        time = time + L
    End If
    direction = 1 - direction
    R = R - 1
End While

由于每个event只会处理一次，复杂度为O(Q)。枚举泳道的时间为O(N)，而判定泳道是否可以使用的时间复杂度在O(1)，因此该主函数的时间复杂度为O(NQ)。在可接收范围内。