A
直接暴力DP的状态数是O(n*4^12)的,这样会超时。
我们可以对每一个二进制位记录一个值,当这个值为2的时候,表示所有选出来的数中,这一位都是1;对于其它情况,如果选出来的数有奇数个1,那么值为1,否则就为0。
不难发现按照上述状态进行DP,只要再记录一下选出来的数的个数的奇偶性,就能从状态中直接得到选出来的所有数的异或值和and和,这样状态数就缩减到了O(n*3^12),就能过了。
B
先把所有数从小到大排序,接着可以枚举中位数是哪两个数的平均数,假设是l和r(长度为奇数的情况相当于l=r),然后我们给数列中所有数减去平均数,那么这时的方案数就等于从[1,l),(r,n]这两个区间中选出相同数目的数使得它们的和小于0。
我们可以把待选的数给单独拿出来(即把区间[l,r]的数删掉),如果原来它的下标小于l,把么权重为1否则权重为-1。问题就相当于给出若干个数,你要选出一些数使得它们的权重和为0且权值和小于0,这是一个经典的meet in middle的问题。我们可以把数均等的分成两部分,分别处理出两部分中的所有选取方法,然后根据权重分组,每组排序之后就能统计答案了。
上述算法的时间复杂度是 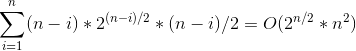
这样是会超时的(除非你的常数足够好)。
我们发现我们没有必要排序,我们可以在枚举的时候使用归并的方法,直接让每组有序,这样就能减少一个n的复杂度。
C
显然如果一张子图的权值不是0,那么在这张子图中最多只有一个简单环。
考虑没有环的情况,我们要统计的就是这张图的所有生成森林的权值和。统计最小生成树个数有一个传统的基尔霍夫矩阵的做法,不难发现只要添加一个虚点,往所有节点都连一条边,那么新图的最小生成树个数就是原图所有生成森林的权值和。
现在考虑恰好有一个环的情况,这也是一个经典问题,我们可以先枚举环上的点集。一个点集组成一个环的方案数可以用一个O(2^nn^2)的DP求出,接着我们可以把这个环缩成一个点,然后就转化成生成森林的问题了(注意在缩成点之后新增加的虚点要向这个位置连环的大小条边)。
时间复杂度O(2^nn^3)
D
可以参考WC2016上的营员交流《segment tree beats》,在这个上面介绍了一种把区间取max,区间取min操作转化成区间加减操作的方法(但是上面的复杂度分析略有问题)。
考虑只有区间加减,显然被影响到的区间中的所有数都被修改了(要注意特判加0的情况),只需要区间加一就行了。
所以现在我们可以在线段树上把最小值、最大值、同时不是最大值和最小值这三类数分开来统计,要注意在边界情况下可能会有一些细节问题。
时间复杂度O(mlog^2n)

A题能否贴份代码链接。。 好理解些。。rank榜出题的代码并看不懂。。