题目大意

Question

18

11

题目大意

现在有一场持续时间为M的游乐会，在游乐会上有N种不同的表演节目，同一时间只能有一个节目进行表演。

每种节目最多可以表演K次，且每种节目具有自己的三个属性值a[i],b[i],c[i]。

当一个节目在时间剩余p开始时，它会产生a[i]-(M-p)*b[i]的价值，这个节目会持续c[i]个单位时间。

此外由于最后有结束致辞，所以需要空出最后1个单位时间。

求问，怎么安排表演节目，可以使得产生的总价值最大。

解题思路

首先可以确定，本题是一道动态规划的题目。

每个物品计算其价值的函数为y = a[i] - (M - p) * b[i]，在这个函数中只有p一个变量，其他均为常数。因此我们可以写成一个y关于p的函数：

y = f(p) = a[i] - M * b[i] + p * b[i]

f(p)由两个部分组成： - a[i] - M * b[i]是一个固定的值，只与活动本身的属性有关。记为A部分 - p * b[i]是随时间变化的值，与活动的开始时间有关。记为B部分

当我们已经选择好一系列活动之后，这些活动的A部分价值也就确定了。而我们要关心的是如何排序这些活动，使得B部分价值最大。

假设我们已经选好了k个活动，编号为1..k(注意，这里的编号和题目里面的种类序号不同)。记第i个活动开始的剩余时间为p[i]，该活动对应的b值为b[i], c值为c[i]。

则B部分的总价值为：sigma(p[i]*b[i])

考虑能否找到一个性质，使得能够找到一种顺序使得B部分的值达到最优。

我们先来看看交换两个相邻的活动，会对结果造成怎么样的影响：

i,j是两个相邻的活动，i的剩余时间为p。由于交换i,j并不会影响到其他活动的开始时间，会改变的只有p[i]和p[j]。

交换前：

p[i] = p, p[j] = p - c[i]
v1 = p * b[i] + (p - c[i]) * b[j]

交换后：

p[i] = p - c[j], p[j] = p
v2 = (p - c[j]) * b[i] + p * b[j]

因此差值delta = v2 - v1:

delta = (p-c[j])*b[i] + p*b[j] - p*b[i] - (p-c[i])*b[j]
      = c[i]*b[j] - c[j]*b[i]

若delta>0，则交换i,j可以使得B部分总价值最大。

将delta>0换一个形式表示：

delta = c[i]*b[j] - c[j]*b[i] > 0
=> c[i]*b[j] > c[j]*b[i]
=> b[j]/c[j] > b[i]/c[i]

不妨设d[i]=b[i]/c[i]，可以发现，若两个活动i,j相比，d值大的活动放在前面一定比较优。

又由于b,c均为活动本身的固定属性，每一种活动的d值也即是固定的。

因此我们得到一个性质：

将所有种类的活动按照b[i]/c[i]从大到小排序后，排名越在后面的活动越应该放在后面进行。

同时我们可以将原问题转化为一个背包问题。

把时间M看做背包的容积，N种活动看成N种不同物品。

由于每个活动的价值是跟开始时剩余时间P相关，可以理解成：当我们放入这个物品时，背包已使用的空间决定了这个物品的价值。

因为后枚举的物品d值一定是最大的，所以我们假设这个物品就是最后放入背包的。

像这样一个物品的价值是由一个函数f(x)来决定的背包问题，我们称它为泛化物品背包问题。

同时在本题中每一个活动可以选择K次，因此我们需要枚举放入几个该物品，像这样的问题我们称为多重背包问题。

所以本题实质是一个多重泛化物品背包问题。

一个解决的伪代码为：

sort() // 将活动按照b/c的值，从大到小排序
For i = 1 .. N // 枚举活动种类
    For v = c[i] .. M-1 // 枚举背包容量
        For j = 1 .. K // 枚举举办次数
            totalTime = c[i] * j
            If (totalTime > v) Thne
                // 举办j次，超过了背包容量
                Break
            End If
            tempValue = calc(v - totalTime, j, i)
            // 计算从v - totalTime开始连续进行j次活动i的得到的价值
            // 这个可以用数学方法进行计算，因此时间复杂度为O(1)
            If (f[i][v] < f[i - 1][v - totalTime] + tempValue) Then
                f[i][v] = f[i - 1][v - totalTime] + tempValue
            End If
        End For
    End For
End For

该算法在时间复杂度O(KMN)，对于题目给出的数据范围，可以肯定会超过时间限制，还需要进一步优化。

在上面的循环中，我们枚举了最后一次活动结束时间，也即是背包容量v。由于每一次活动持续的时间均为c。因此固定v之后，我们考察的f[i-1][v']+tempValue中的v'一定是v减去整数倍的c，即：

v' = v - k*c (k≥1)

将v'排序，并加上v刚好构成一个序列：v-k*c,v-(k-1)*c, ... , v-2*c, v-c, v

这个数列的值有一个共同的特点，就是他们模c同余。

所以我们不妨用一个数组q[r][]来按顺序记录所有模c余r的容量v。

将这个改动放入伪代码中为：

sort() // 将活动按照b/c的值，从大到小排序
q[][] = 0 // 将q[]设置为0
tail[] // tail[r]表示q[r]中保存的数字个数

For i = 1 .. N // 枚举活动种类
    tail[] = 0 // 将tail数组重置
    For v = c[i] .. M-1 // 枚举背包容量

        r = v % c[i]    // 得到余数r
        tail[r] = tail[r] + 1
        q[r][tail[r]] = v   // 将v放置于当前数组的最后一位

        t = tail[r] - 1
        while (t > 0 && (v - q[r][t]) / c <= K)
            // 检查到该时间点，活动举办的次数是否大于K
            tempValue = calc(q[r][t], v, i)
            // *注意这里计算价值函数改变了*
            // 计算从q[r][t]开始连续到时间v，连续进行活动i的得到的价值
            // 这个可以用数学方法进行计算，因此时间复杂度为O(1)
            If (f[i][v] < f[i - 1][ q[r][t] ] + tempValue) Then
                f[i][v] = f[i - 1][ q[r][t] ] + tempValue
            End If
        End While
    End For
End For

再加入q[r][]之后，我们可以通过这个数组来观察每个转移点v'的f[i - 1][v']+tempValue，不妨用直方图来表示每一个v'所对应的f[i - 1][v']+tempValue：

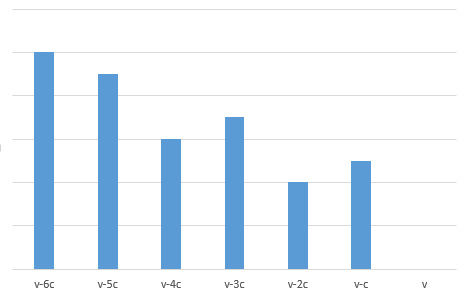
每一个蓝色的矩形对应了这个点的f[i-1][v']+tempValue值。

当我们枚举到v+c时，计算v'转移到v+c等于计算了v'转移到v再加上v~v+c这段时间进行了一次i活动。因此对于v+c的图来说，等于是在上图的基础上，全部增加一个相同的a[i]-(M-v)*b[i](橙色的部分)：

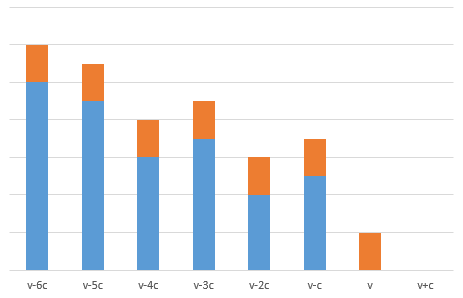
可以观察到，在处理v时，选择v-c的值是优于v-2c的。即使v-c的值等于v-2c，也因为v-c举行的活动次数较少，而认为v-c更优。同理，在处理v+c时，v-c和v-2c的相对大小也没有变化，v-c仍然优于v-2c。因此v-2c在得到v-c之后，无论如何都不会再用到。所以此时我们可以抛弃掉v-2c这个点。同样的还有v-4c这样的点。

当我们将所有类似v-2c和v-4c的点都删去之后，可以得到图：

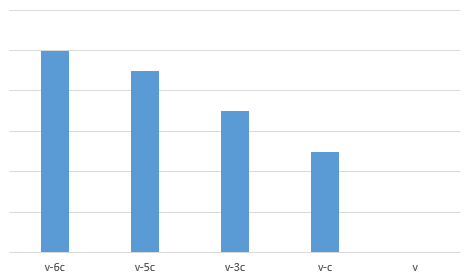
对于新的这个图，它有如下的性质： - 满足严格的单调性 - 任意一个v，其左边的点都是在计算它时需要枚举的点

我们可以通过计算相邻两个v'的值，去维护q[r][]满足这个单调性。而满足这种单调性的队列，我们称之为单调队列。

在维持单调队列的情况下，枚举到某个v时，最优的结果显然就是最左边的点。因此我们不需要去从右到左依次枚举每一个可能的转移点，而直接选取最左的点即可。查找转移点的时间复杂度从O(K)降低至O(1)。

并且由于每个转移点只会进一次单调队列，出一次单调队列。所以维护单调队列的均摊时间复杂度为O(1)。

此外还需要注意，在本题中由于每个活动最多只能举行K次，所以转移点最多只能是v-k*c。所以我们除了需要维护队列末尾的tail之外，还需要一个维护队列头的head。当q[r][head[r]]的值小于v-k*c时，需要将head进行右移。

因此加入维护单调队列代码之后的伪代码为：

sort() // 将活动按照b/c的值，从大到小排序
q[][] = 0 // 将q[]设置为0
tail[] // tail[r]表示q[r]中保存的数字个数

For i = 1 .. N // 枚举活动种类
    tail[] = 0 // 将tail数组重置
    head[] = 1 // 将head数组重置为1
    For v = c[i] .. M-1 // 枚举背包容量

        r = v % c[i]    // 得到余数r
        tail[r] = tail[r] + 1
        q[r][tail[r]] = v   // 将v放置于当前数组的最后一位

        while (tail[r] > head[r]) {
            tempValue1 = calc(q[r][ tail[r] ], v, i)
            // 计算从q[r][ tail[r] ]开始到时间v一直进行活动i的得到的价值
            // v - q[r][ tail[r] ] 一定能够整除c
            value1 = f[i - 1][ q[r][tail[r]] ] + tempValue1

            tempValue2 = calc(q[r][ tail[r]-1 ], v, i)
            value2 = f[i - 1][ q[r][tail[r]-1] ] + tempValue2
            // 同样计算出前一个点

            If (value1 >= value2) Then
                // 可以抛弃tail[r]-1这个点了
                q[r][ tail[r] - 1 ] = q[r][ tail[r] ]
                tail[r] = tail[r] - 1
                // 用tail[r]覆盖掉原来的tail[r]-1
            Else
                Break
                // 该处满足单调性质，由于前面一直用同样的方法处理
                // 所以前面的部分也满足单调性质，因此可以直接退出循环
            End If
        }

        While ((v - q[r][ head[r] ]) / c[i] > K)
            head[r]++
            // 处理左边边界
        End While

        tempValue = calc(q[r][ head[r] ], v, i)
        f[i][v] = f[i - 1][ q[r][head[r]] ] + tempValue
    End For
End For

Result = max(f[N][])
// 最优值是f[N][0 .. M-1]中最大的一个

由此，整个算法的时间复杂度降低为O(NM)，空间复杂度为O(NM)。对于给定的数据范围也就能够顺利通过了。

asked 2016-03-26

gtdzx

0