题目大意

小Hi和小Ho最近在研究内存分配的机制，他们写了一个比较简单的内存。内存可以表示成M个连续的存储空间，下标为0..M-1：

每当有数据写入时，内存分配程序会从下标0开始向右找一块足够存放下该数据的区域，将该数据写入。比如写入一个长度为2的数据，因为是第一个数据，我们用1来表示：

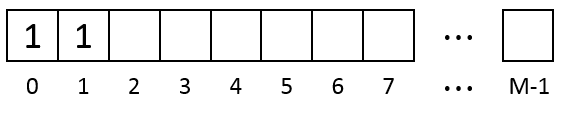
之后继续依次写入长度为3的数据和长度为2的数据，则有：

当数据足够多后，我们可能会遇到剩下的空间不足以写下新的数据。这时内存程序会从最早的数据开始进行删除。假设我们现在写到第8个数据把内存写满了：

这时我们需要写入第9个数据，该数据长度为4。则内存程序会删掉第1个数据：

但是仍然不够，于是删除掉第2个数据。这时就足够放下第9个数据了。于是内存程序存下第9个数据：

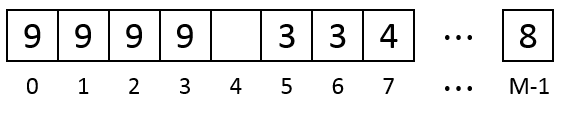
当有足够的空间存放数据数，数据总是尽可能靠左(起点下标尽可能小)存放。

小Hi和小Ho写好了内存之后，打算测试一下。他们会连续写入的N个数据，在所有数据写入完成后，他们想知道现在内存中各个存储单元的情况。

解题思路

一个简单的思路是我们使用长度为M的数组来模拟整个内存使用的情况。

对于其中60%的数据：1≤N≤200，10≤M≤100，1≤K[i]≤5，这种简单的方法是可行的。

而对于另外40%的数据，由于M的长度最大可能为10^9，显然无法处理，因此我们需要进一步优化。

通过对简单数据的分析，我们可以发现这样一个情况：

一个相同的数字总是占用了一段连续的内存。

那么我们可以使用(a,b)来表示一段长度为b的数字a，我们把这样表示的一段数据叫做一个数据块。

比如内存情况1 1 1 1 1 2 2 3 3 0，则可以表示为：

(1,5),(2,2),(3,2),(0,1)

那么在简化的表示方法之下，我们应该如何来进行内存上的操作呢？

• 添加一个数据(i, k[i])

在内存中寻找最左边的(0, b)，同时满足b≥k[i]。

若b>k[i]，将(0，b)分割为两个数据块(i, k[i]),(0, b-k[i])

若b=k[i]，将(0，b)直接改为(i, b)

记录第i个数据对应的(i, k[i])的位置，方便删除

• 删除一个数据(i, k[i])

根据记录，找到到i的数据块(i, k[i])，同时找到其前一个块(prev, k[prev])和后一个块(next, k[next])

若prev=0，讲(prev, k[prev])合并至(i, k[i])

若next=0，讲(next, k[next])合并至(i, k[i])

将(i,k[i])置为(0,k[i])

由于在简化的表示下，内存最多有2N个块，因此即便是顺序查找一个满足b≥k[i]的(0, b)数据块，需要的时间复杂度也不超过O(N)。

而删除操作借助已经记录的数据位置，实现的时间复杂度为O(1)。

根据题目，最多可能添加N个数据块，因此总的时间复杂度为O(N^2)，可以解决问题。

有了算法，接下来就是考虑如何使用代码实现，这里我们采用链表来做：

对于每一个数据块，我们用如下方式表示：

Block {
    key: 表示数据编号，对应(a,b)中的a
    length: 表示数据长度，对应(a,b)中的b
    prev: 表示该数据块的前一个块
    next: 表示该数据块的后一个块
}

由于每一个块都有前后指针，因此为了简化处理，我们给链表加上头尾两个哨兵节点，得到初始的链表状态为：

(-1, 0), (0, M), (-1, 0)

初始化为：

init(M):
    head = new Block
    head -> key = -1
    head -> length = 0
    head -> prev = NULL
    head -> next = NULL

    p = new Block
    p -> key = 0
    p -> length = M
    p -> prev = head
    p -> next = NULL
    head -> next = p

    p2 = new Block
    p2 -> key = -1
    p2 -> length = 0
    p2 -> prev = p
    p2 -> next = NULL
    p -> next = p

这样就将初始的三个节点加入了链表，接下来就是几个操作。

• 查找

直接按顺序进行扫描，查找符合要求的(0, b)

findEmpty(len):
    p = head -> next
    While (p -> key != -1)
        If (p -> key == 0 && p -> length >= len) Then
            Return p // 找到合适的空内存段
        End If
        p = p -> next
    End While
    Return NULL // 找不到空的内存

• 添加

通过findEmpty找到的空数据块，并进行插入操作

insert(emptyBlock, key, len):
    // emptyBlock是找到的符合要求的空数据块
    If (emptyBlock -> lenght == len) Then
        emptyBlock -> key = key
    Else
        p = new Block // 新的(0, b - k[i])
        p -> key = 0
        p -> length = emptyBlock -> length - len

        p -> prev = emptyBlock
        p -> next = emptyBlock -> next
        p -> next -> prev = p

        emptyBlock -> key = key
        emptyBlock -> length = len
        emptyBlock -> next = p
    End If
    pos[ key ] = emptyBlock // 记录第key个数据的位置

• 删除

通过pos[key]来获取数据块

delete(key):
    p = pos[ key ]

    tp = p -> prev // 合并前一个
    If (tp -> key == 0) Then
        p -> length = p -> length + tp -> length
        p -> prev = tp -> prev
        p -> prev -> next = p
        Delete tp
    End If

    tp = p -> next // 合并后一个
    If (tp -> key == 0) Then
        p -> length = p -> length + tp -> length
        p -> next = tp -> next
        p -> next -> prev = p
        Delete tp
    End If

    p -> key = 0

• 主函数

如下

main()
    Input N, M
    init(M)
    lastDeleteData = 0
    For i = 1 .. N
        Input K
        While (true)
            p = findEmpty(K)
            If (p != NULL) Then
                insert(p, i, K)
                Break
            Else
                lastDeleteData = lastDeleteData + 1
                delete(lastDeleteData)
            End If
        End While
    End For
    //Type Ans 最后根据链表输出结果

本题在这次笔试中是作为中等偏简单的题目设计的，所以时间复杂度在O(N^2)的算法就能够拿满分。 而实际上本题还有O(NlogM)的线段树算法，这里留作大家思考。 如果你用O(NlogM)的线段树算法AC了这道题，欢迎跟帖分享。